Pappus's hexagon theorem
In mathematics, Pappus's hexagon theorem (attributed to Pappus of Alexandria) states that given one set of collinear points A, B, C, and another set of collinear points a, b, c, then the intersection points X, Y, Z of line pairs Ab and aB, Ac and aC, Bc and bC are collinear. (Collinear means the points are incident on a line.) It holds in the projective plane over any field, but fails for the projective plane over any non-commutative division ring.[1]
The dual of this theorem states that given one set of concurrent lines A, B, C, and another set of concurrent lines a, b, c, then the lines x, y, z defined by pairs of points resulting from pairs of intersections A∩b and a∩B, A∩c and a∩C, B∩c and b∩C are concurrent. (Concurrent means that the lines pass through one point.)
Pappus's theorem is a special case of Pascal's theorem for a conic, in the limiting case when the conic degenerates into 2 straight lines.
The Pappus configuration is the configuration of 9 lines and 9 points that occurs in Pappus's theorem, with each line meeting 3 of the points and each point meeting 3 lines. This configuration is self dual. The Levi graph of the Pappus configuration is the Pappus graph, a bipartite distance-regular graph with 18 vertices and 27 edges.
Contents |
Proof
Pappus's theorem is equivalent to its dual (in the presence of the basic axioms for a projective plane). The dual of Pappus's theorem can be proved for the projective plane over any field using projective coordinates as follows.
The dual of the theorem states that if all but one of the nine sets of three lines are concurrent, then all of them are. Choose projective coordinates with
- C=(1,0,0), c=(0,1,0), X=(0,0,1), A=(1,1,1).
On the lines AC, Ac, AX, given by x2=x3, x1=x3, x2=x1, take the points B, b, Y to be
- B=(p,1,1), b=(1,q,1), Y=(1,1,r)
for some p, q, r. The three lines XB, cb, CY are x1=px2, x2=qx3, x3=rx1, so all pass through the same point (called a in the diagram) if and only if pqr=1. The condition for the three lines Cb, cB and XY x2=qx1, x1=px3, x3=rx2 to pass through the same point (Z in the diagram) is qpr=1. So this last set of three lines is concurrent if all the other eight sets are because multiplication is commutative, so pqr=qpr, which proves the dual of Pappus's theorem.
The proof above also shows that if Pappus's theorem holds for a projective space over a division ring, then the division ring is a (commutative) field. German mathematician Gerhard Hessenberg proved that Pappus's theorem implies Desargues's theorem.[2] In general, Pappus's theorem holds for some projective space if and only if it is a projective space over a commutative field. The projective spaces in which Pappus's theorem does not hold are projective spaces over non-commutative division rings, and non-Desarguesian planes.
Other Statements of Pappus's Theorem
In addition to the above characterizations of Pappus's Theorem and its dual, the following are equivalent statements:
- If the six vertices of a hexagon lie alternately on two lines, then the three points of intersection of pairs of opposite sides are collinear.[3]
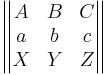 In a matrix of 9 points (as in the picture and description above), if the first two rows and the six "diagonal" triads are collinear, then the third row is collinear. That is, if ABC, abc, AbZ, BcX, CaY, XbC, YcA, and ZaB are all lines, then Pappus's theorem states that XYZ must be a line. Also, note that the same matrix formulation applys when A, B, C and a, b, c are concurrent lines in the dual form of the theorem.[4]
In a matrix of 9 points (as in the picture and description above), if the first two rows and the six "diagonal" triads are collinear, then the third row is collinear. That is, if ABC, abc, AbZ, BcX, CaY, XbC, YcA, and ZaB are all lines, then Pappus's theorem states that XYZ must be a line. Also, note that the same matrix formulation applys when A, B, C and a, b, c are concurrent lines in the dual form of the theorem.[4]- Given three distinct points on each of two distinct lines, pair each point on one of the lines with one from the other line, then the joins of points not paired will meet in (opposite) pairs at points along a line.[5]
- If two triangles are doubly perspective, then they are trebly perspective.[2]
- If AB, CD, and EF are concurrent and DE, FA, and BC are concurrent, then AD, BE, and CF are concurrent.[4]
Notes
References
- Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50458-0, MR123930
- Whicher, Olive (1971), Projective Geometry, Rudolph Steiner Press, ISBN 0-85440-245-4